IEIP_Note

Data Structure, 자료구조

컴퓨터 상 자료를 효율적으로 저장하기 위해서 만들어진 논리적인 구조
자료구조의 현명한 선택을 통해 효율적인 알고리즘을 사용할 수 있게 하여 성능 향상 시킴
자료구조는 크게 선형 구조와 비선형 구조로 나뉜다.

구조	설명	종류
선형 구조 Linear	데이터를 연속적으로 연결한 자료구조 자료를 구성하는 원소들을 하나씩 순차적으로 나열한 형태	리스트, 스택 큐, 데크
비선형 구조 Non-Linear	데이터를 비연속적으로 연결한 자료구조 하나의 자료 뒤에 여러 개의 자료가 존재할 수 있는 형태	트리, 그래프

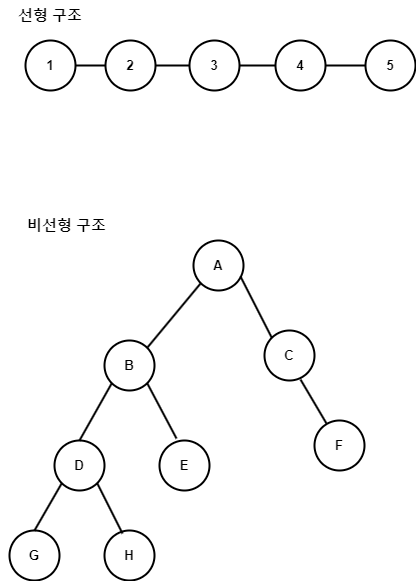
선형 구조 / 리스트 List

선형 리스트 Linear List
- 배열과 같이 연속되는 기억 장소에 저장되는 리스트
- 대표적인 선형 리스트: 배열 Array
- 가장 간편한 자료구조, 접근 구조가 빠르다.
- 자료의 삽입, 삭제 시 기존 자료의 이동이 필요함.
연결 리스트 Linked List
- Node의 Pointer 부분으로 서로 연결한 리스트
- 연결 방식에 따라 단순 연결 리스트, 원형 연결 리스트
  이중 연결 리스트, 이중 원형 연결 리스트로 구분된다.
- Node의 삽입, 삭제가 선형 리스트와 달리 편리한 편이다.
- 연결을 위한 Pointer가 추가되어 저장 공간이 추가로 필요하고
  Pointer 통해서 찾는 시간이 추가됐기 때문에 선형 리스트에 비해 느린 편이다.

선형 구조 / 스택 Stack

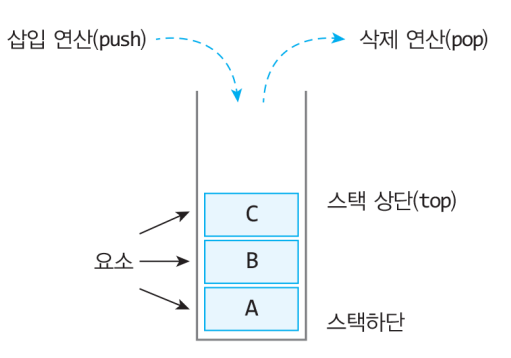
한 방향으로만 자료를 넣고 꺼낼 수 있는 LIFO 형식의 자료구조
LIFO => Last In First Out, 마지막에 넣은 것이 먼저 나간다.
한 방향으로만 PUSH와 POP 이용하여 자료를 넣고 꺼낸다.
스택의 가장 위에 있는 데이터는 TOP이라고 하며
Stack Pointer라고도 부른다.
PUSH 연산 : 데이터를 차례대로 스택에 추가하는 연산
POP 연산 : 스택에서 가장 위에 있는 데이터를 하나씩 꺼내는 연산
이러한 자료구조 스택은 인터럽트 처리, 함수 호출
후위 표현 연산 (수식 계산), 깊이 우선 탐색 (DFS)에서 응용할 수 있다.

스택 운용 분야	설명
인터럽트 처리	현재 진행 중인 명령어 위치를 스택에 `Push` 인터럽트 발생 상황을 처리한 후, 인터럽트 전에 진행 중이던 명령어 위치를 스택에서 `Pop` 통해서 받아온다.
함수 호출 (재귀함수 포함)	함수 호출 시, 현재 진행 중인 명령어 주소를 스택에 이양한다.
후위 표현 연산	`Postfix` 계산할 때 사용
깊이 우선 탐색 Depth First Search	깊이 내려갈 때마다 스택에 값을 `Push`하고 더이상 깊이 내려갈 곳이 없으면 스택에서 `POP`한 node와 인접한 node를 탐색한다.

선형 구조 / 큐 Queue

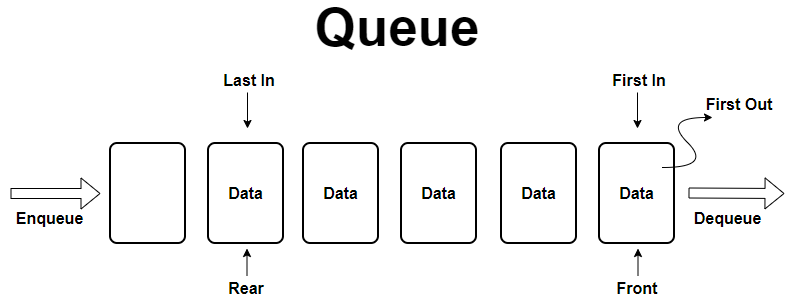
한쪽 끝에서 삽입 작업이 이뤄지고, 반대쪽 끝에서는 삭제 작업이 이뤄지는
First In First Out 형식의 자료구조를 말한다.
한 방향에서는 ENQUEUE 연산을 이용하여 데이터 입력이 이뤄지고
다른 쪽 방향에서는 DEQUEUE 연산을 이용하여 데이터 출력이 이루어진다.
데이터를 꺼내는 쪽, 출력 부분에 가장 가까운 쪽을 Front
데이터를 넣는 쪽, 입력 부분에 가장 가까운 쪽을 Rear라고 한다.
ENQUEUE : 데이터를 차례대로 넣는 연산
DEQUEUE: 처음 저장된 데이터부터 하나씩 꺼내는 연산
큐는 운영체제의 작업 Scheduling, 메시지 전송 분야에서 활용할 수 있다.

Queue 응용	설명
운영체제 작업 Scheduling	작업이 자원을 할당 받기 전까지 대기
메시지 전송	메시지를 한 곳에서 다른 한 곳으로 전송하는 동안 일시적으로 보관

선형 구조 / 데크 Deque

Deque == Double Ended Queue
큐의 양쪽 끝에서 삽입과 삭제를 할 수 있는 자료구조

두 개의 Pointer 사용하여, 양방향에서의 삽입 / 삭제가 가능하다.
Deque 이용한 Stack과 Queue 구현하는 것도 가능하다.
PUSH 연산을 통해 큐의 양쪽 끝에서 데이터의 삽입을 진행하고
POP 연산을 통해 Deque의 Front와 Rear에 있는 데이터를 하나씩 꺼낼 수 있다.

비선형 구조 / 트리 Tree

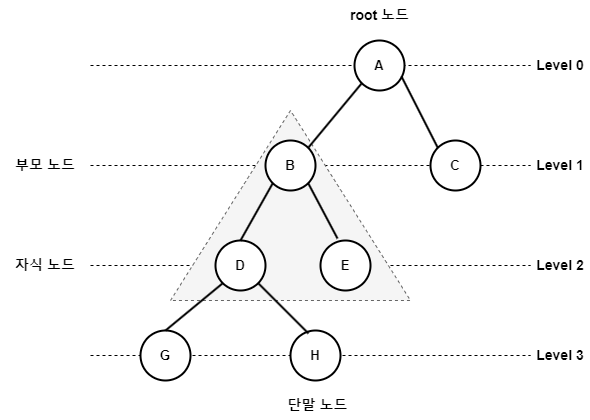
데이터를 계층화시킨 자료구조
Graph의 특수한 형태
Node와 Branch (선분)으로 되어 있고, 정점 사이에 Cycle이 형성되어 있지 않고
자료 사이의 관계성이 계층 형식으로 나타나는 비선형 구조이다.
Index 조작하는 방법으로 가장 많이 사용하는 자료구조
Node와 각 Node를 연결하는 Link로 구성됐다.
배열과 달리 Node들이 Pointer로 연결되어 있기 때문에
Node의 상한선이 없다.

Tree 용어	설명
root node	트리에서 부모가 없는 최상위 노드 트리의 시작점 root node = { `A` } (상단 예시 기준)
Leaf node 단일 노드	자식이 없는 노드, 트리 가장 말단에 위치함 단일 노드 = { `G`, `H`}
Level	루트 노드를 기준으로 특정 노드까지 경로 길이 `D` 노드의 Level = 3
Parent Node	특정 노드에 연결된 이전 레벨의 노드 `D`와 `E` 노드의 부모 = { `B` }
Child Node	특정 노드에 연결된 다음 레벨의 노드 `B`의 자식 = { `D`, `E` }
Sibling 형제 노드	같은 부모를 가진 노드 `G`와 `H`는 `D`라는 같은 부모 노드를 지닌 형제 노드이다.
Depth 깊이	루트 노드에서 특정 노드에 도달하기 위한 간선의 수 트리 깊이 = 3
Degree 차수	트리 구조에서 각 노드가 가진 가지 수 (서브 트리 개수) `D` 노드의 차수 = 2

트리 순회 방법

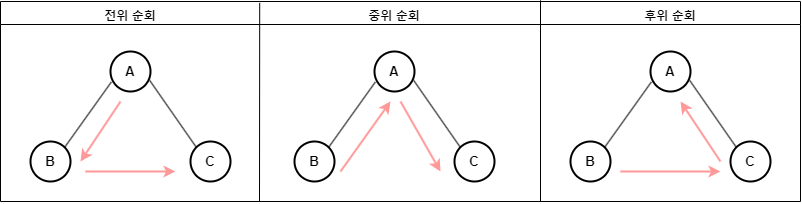
트리 순회 방법은 전위 순회, 중위 순회, 후위 순회로 나뉜다.

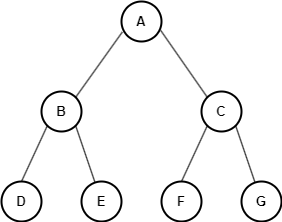
트리 순회 설명용 이미지
전위 순회 Pre-Order
- 먼저 root 노드를 방문하고 이어서 왼쪽 서브 트리를 방문한 후
  오른쪽 서브 트리를 방문하는 순으로 순회하는 방식
- root → left → right 순으로 방문한다.

전위 순회 설명 / 상단 이미지 활용

- 위의 이미지를 기준으로 제일 먼저 root 노드인 `A` 방문한다.
- 이어서 왼쪽 서브 트리를 `B` - `D` - `E` 순으로 방문하고
- 마지막으로 오른쪽 서브 트리를 `C` - `F` - `G` 순으로 방문한다.

=>`A` → {`Left` / `B` → `D` → `E`} → {`Right` / `C` → `F` → `G`}

중위 순회 In-Order
- 먼저 왼쪽 서브 트리를 중위 순회한 후, 제일 상단의 root 노드를 방문한다.
  그 이후, 오른쪽 서브 트리를 중위 순회하는 방식
- left → root → right 순으로 순회한다.

중위 순회 설명 / 상단 이미지 활용

- 중위 순회는 Left - root - Right 순으로 방문하는 순회 방식이다.

- 제일 먼저 왼쪽 서브 트리를 순회하는데, 왼쪽 자식 노드인 D를 먼저 방문하고
  이어서 부모 노드인 B를 거친 뒤 다른 자식 노드인 E를 순회한다. (D → B → E)
  
- 왼쪽 서브 트리 순회를 마치면, 제일 상단의 root 노드인 A를 방문하고
  이어서 오른쪽 서브 트리 순회를 시작한다.

- 오른쪽 서브 트리도 부모 노드인 C를 먼저 방문하고
  이후 자식 노드 F → G 순으로 중위 순회한다. { Right / C → F → G}

=> 결과: D → B → E → A → F → C → G

후위 순회 Post-Order
- 먼저 왼쪽 서브 트리를 후위 순회하고, 이어서 오른쪽 서브 트리를 후위 순회한 뒤
  마지막으로 제일 상단의 root 노드를 방문하는 순회 방식이다.
- Left → Right → root 순으로 순회한다.

후위 순회 설명 / 상단 이미지 활용

- 후위 순회는 Left - Right - root 순으로 방문하는 순회 방식이다.

- 제일 먼저 왼쪽 서브 트리의 단일 노드 D → E 순으로 방문하고
  이어서 부모 노드인 B를 방문한다. (D → E → B)
- 그 다음 오른쪽 서브 트리로 넘어가서, 단일 노드 F → G 순으로 방문하고
  이어서 부모 노드인 C를 방문한다. (F → G → C)
- 그리고 마지막으로 남은 제일 상단의 root 노드인 A 노드를 방문하는 후위 순회를 한다.

=> 결과: D → E → B → F → G → C → A

비선형 구조 / 그래프 Graph

Node와 노드를 연결하는 간선 Edge를 하나로 모아 놓은 자료구조
Tree == Cycle이 없는 그래프
그래프는 방향성의 유무에 따라 방향 그래프와 무방향 그래프로 나뉜다.

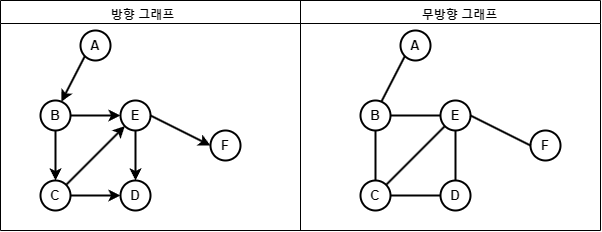
그래프의 탐색 방법은 깊이 우선 탐색, 너비 우선 탐색
두 가지의 탐색 방법이 존재한다.
깊이 우선 탐색 Depth First Search, DFS
- 최대한 깊이 내려간 뒤, 더이상 내려갈 곳이 없으면 옆으로 이동하는 방식
너비 우선 탐색 Breadth First Search, BFS
- 최대한 넓게 이동한 다음, 더이상 갈 수 없을 때 아래로 이동하는 방식